Uno speciale per la giornata del Pi greco

Il π (Pi greco) è il simbolo della Matematica per antonomasia. È il rapporto tra la lunghezza di una circonferenza e il suo diametro, ovvero la misura dell’area di un cerchio di raggio 1, ovvero la misura della superficie di una sfera di diametro 1. Emerge in situazioni imprevedibili, destando meraviglia, ad esempio:
– come limite della somma dei reciproci dei quadrati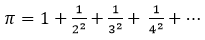
– nell’identità di Eulero  che è stata giudicata la formula matematica più poetica, da un sondaggio condotto sui lettori del The Mathematical Intelligencer nel 1990, perché lega l’operazione esponenziale a tutti i principali simboli matematici: il simbolo di uguaglianza, quello della somma, lo zero, l’uno, e le costanti, base dei logaritmi naturali e che rappresenta il numero immaginario 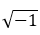Questa formula si giustifica dalla definizione ma ha un’interpretazione naturalissima, ci dice che per andare dalla parte opposta della città possiamo percorrere metà della circonvallazione!

Forse la più sorprendente apparizione di π è quella suscitata dal Conte Buffon che nel XVIII secolo, calcolò che il reciproco di π è la frequenza con la quale uno stuzzicadenti, lungo la metà della larghezza delle assi del parquet del suo studio, cadendo a caso, incrociava la fuga tra due assi. Cosa vi è di più semplice o più prosaico di ciò? Basta un po’ di maleducazione nel gettare lo stuzzicadenti, per definire π.

Lo scorso 5 agosto i ricercatori dell’Università delle Scienze Applicate dei Grigioni in Svizzera hanno annunciato di aver calcolato il valore di con l’approssimazione di 62,8 bilioni di cifre esadecimali, mediante un programma per computer che ha girato per circa 1 mese.  Ovvero hanno calcolato 62,8×10¹² cifre con una notazione per i numeri nella quale si usano 16 cifre da zero a diciassette, cioè 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F. Questo risultato ha permesso loro di entrare nel Guinness dei primati, in quanto il numero di cifre di π precedentemente conosciute erano “solamente” di 50×10¹² (senza togliere nulla ai ricercatori svizzeri, incidentalmente, vi ricordo la discussione su Josway circa la problematicità nel convincersi della correttezza di un programma).

Il numero π pervade tutta la matematica e le sue applicazioni, anche dove non lo si immaginerebbe. Serve conoscere un valore abbastanza preciso di π per effettuare le giuste correzioni ai sistemi GPS dovute agli effetti della gravitazione universale di Einstein. Serve conoscere un valore abbastanza preciso di π per rendere efficienti gli algoritmi per la compressione dei dati basati sull’analisi armonica e le trasformate di Fourier, impiegati ad esempio dai sistemi di trasmissione della musica e delle immagini in streaming.

È legittimo, però, chiedersi: a cosa serve conoscere tante cifre quante ne hanno calcolate i ricercatori dei Grigioni? È difficile immaginare una qualche applicazione real-life nella quale servano più di una ventina di cifre decimali di π. Ad esempio è stato dimostrato che per il calcolo astronomico del volume dell’universo con l’approssimazione de diametro di un atomo di idrogeno, 39 cifre decimali esatte sono più che sufficienti. Insomma, in una visione essenzialmente utilitaristica, anche conoscere già 1000 cifre di π sarebbe uno spreco computazionale.

Cercherò quindi di dare alcune motivazioni per giustificare il fascino di questa ricerca, al di là del valore della prestazione computazionale degli informatici svizzeri, che è indubbiamente straordinaria, se si pensa che il matematico dilettante inglese William Shanks impiegò molti mesi del 1873 per calcolare 707 cifre delle quali solo le prime 527 erano corrette.

Fate attenzione al prossimo quattordici marzo, poco prima delle quattro di pomeriggio! No, non è solamente il compleanno di Albert Einstein. Osservate bene le cifre che potete utilizzare per descrivere questo momento: 3, 14, 15, 9 … sono proprio quelle dell’incipit di π!  Il 14 marzo è infatti stata denominata Giornata del Pi greco! La sua prima celebrazione si tenne nel 1988 all’Exploratorium di San Francisco, per iniziativa del fisico statunitense Larry Shaw. Nei dieci anni nei quali ebbi il privilegio di essere Sindaco della città di Udine celebrai ogni anno tale ricorrenza organizzando iniziative per festeggiare e promuovere la cultura matematica nelle piazze e scuole della città. L’alfabetizzazione matematica è infatti necessaria per una consapevolezza e resistenza civile a fronte dell’abuso, di dati, percentuali, e previsioni numeriche di cui siamo fatti bersaglio negli ultimi decenni. In foto potete vedere il manifesto della I^a Giornata del π tenuta a Udine nel 2009.

L’iniziativa più folle, ma anche di maggior successo tra le celebrazioni della Giornata del π, è la gara a chi ricorda a memoria il maggior numero di cifre decimali di π. È evidente la necessità di conoscere molte cifre esatte di questo numero per poter dar luogo a tale evento, no? Sul sito, trovate la classifica mondiale di tale prova, e le regole per registrare eventualmente la vostra prestazione. L’indiano Sharma, Suresh Kumar detiene attualmente il record del mondo, impresa realizzata il 21 ottobre 2015 ricordando ben 70.030 cifre decimali esatte in 17 ore e 14 minuti. Il primato italiano è invece detenuto da Luca Valdacca, che il 28 maggio 2020 ha ricordato 22.801 cifre superando così il precedente primato di Nicola Pascolo che, nella Giornata del π del 2012 a Udine, ne ricordò ben 6935. In realtà, in quell’occasione Pascolo scrisse quasi 10.000 cifre, ma la 6936-esima era sbagliata e ciò invalidò tutte le rimanenti che pur erano giuste – ma queste sono le regole della gara. Quell’impresa durò quasi 7 ore.  La foto lo ritrae, primo a sinistra, in quell’occasione, ma la foto mi piace perché illustra quanto sia democratico e non faccia né differenze di genere né di età. Se vi appassionano le gare di memoria date però un’occhiata a quest’altro sito e troverete le graduatorie delle competizioni mnemoniche più impensate.

π si presta a questo tipo di gare perché non è un numero razionale la cui sequenza di decimali dopo la virgola si ripete dopo un po’, oppure risponde a qualche regola facile da calcolare. π è un numero irrazionale le cui cifre decimali compaiono in modo statisticamente casuale, tanto che i matematici congetturano che sia un numero normale, ovvero che nella sua coda tutti i numeri interi occorrano tra le sue cifre con la giusta frequenza, ovvero un decimo i numeri di una cifra, un centesimo quelli di due cifre, e così via. Nella Giornata del π del 2012 a Udine, decidemmo di realizzare la catena umana delle prime mille cifre di π, con i ragazzi delle scuole medie, intorno all’ellisse della Piazza Primo Maggio. Tale piazza si trova nel luogo nel quale Boccaccio ambientò la quinta novella della nona giornata del Decamerone facendovi sorgere il magico “giardino di gennaio bello come di maggio”. Proprio perché tutti congetturano che π sia un numero normale per l’occasione ci procurammo circa 100 magliette per ciascuna delle cifre, in modo da poter raggiungere l’obiettivo, ma nessuno si ricordò di… procurare una maglietta con la “virgola”. Qui a sinistra potete vedere la foto che testimonia quanto sia vero il detto di Flaubert “dieu est dans le detail”, anche se forse lo scrittore francese la intendeva in un altro senso, forse più vicino a quello di Szymborska, di cui parleremo tra breve, rispetto alla legge di Murphy!

Ciò che stupisce di π è che a fronte della naturalezza con la quale si concepisce geometricamente ovvero esteticamente (cosa c’è di più naturale e perfetto di una sfera?), vi sia questa apparente casualità digitale così difficile da afferrare. La storia della scoperta delle cifre di π ha un’origine antica. Possiamo iniziare da Salomone che, in questo caso forse più sbrigativo che sapiente (ma certe volte anche questa è saggezza), usò come valore di π il numero 3 (1Re7,23). I babilonesi usavano un’approssimazione razionale per π data dalla frazione 25/8 (da bambino, mi insegnarono , che è approssimazione migliore). Archimede capì che π era difficile da cogliere con esattezza ed escogitò il metodo di approssimarlo racchiudendo un cerchio tra poligoni regolari inscritti e circoscritti, con numeri di lati via via crescenti. Si stufò nel ripetere l’operazione quando giunse a concludere che π, ovvero il perimetro del cerchio, era compreso tra quello di 2 poligoni rispettivamente di perimetro 3 e 10/70 e 3 e 10/71. Nel 480 Zu Chongzhi trovò un’approssimazione razionale di π sorprendente Ma fu il matematico indiano Mahdava di Sangamagrama che, mille anni dopo, comprese come fosse possibile esprimere molto naturalmente come somma limite della serie infinita:  1 – 1/3 + 1/5 – 1/7 + … (che per eurocentrismo ostinato noi continuiamo a chiamare formula di Leibniz che venne secoli dopo). Questa fu la prima di tantissime e regolarissime sequenze infinite e relazioni notevoli che, oggi sappiamo, π soddisfa e che ci permettono di trattarlo senza che ci si debba smarrire nelle sue cifre.

Perché π ha suscitato tante emozioni? La causa è forse un pregiudizio: ciò che è misurabile è comprensibile mentre l’incommensurabile è inafferrabile. Pregiudizio, che sembra risalire ai pitagorici e all’orrore con il quale accolsero la scoperta che la diagonale di un quadrato non è commensurabile al lato. Si narra che addirittura la morte fosse la pena per chi svelasse la dimostrazione che non è un numero esprimibile come una frazione. L’irrazionale distruggeva irreparabilmente l’illusione che il mondo fosse retto da un’armonia razionale. La commensurabilità, ovvero la proprietà che due quantità siano multiplo intero di una stessa unità di misura (ad esempio due bastoni di lunghezza 1/43 e 1/47 unità, rispettivamente, sono tra loro commensurabili, perché sono multiplo intero di un bastoncino di lunghezza ad esempio 1/2021), sembra concetto elementarissimo. Ma a guardare più a fondo la cosa, la commensurabilità stessa è concetto di complessità illimitata. Un punto su un bastone può condensare l’informazione di tutte le biblioteche del mondo, anche se divide il bastone in due segmenti tra loro commensurabili. È sufficiente che il minimo comune multiplo delle misure dei due pezzi del bastone sia un numero sufficientemente grande. Che un numero possa codificare qualsiasi informazione, compresa quella esprimibile a parole, penso sia ovvio per tutti, essendo alla base della rivoluzione digitale.

Ma quanto tempo ha fatto perdere la natura numericamente irripetibile di π? Basti pensare al problema della quadratura del cerchio, ovvero al problema di costruire un quadrato di area uguale a quella di un cerchio, con esattezza assoluta, utilizzando solamente la riga e il compasso. Ha sedotto matematici, e non, da Euclide fino a Lindeman, che nel 1882 dimostrò essere impossibile (ma molti ancora non si sono rassegnati, però, e continuano a provarci). π è complice inoltre di uno dei più grandi grattacapi dell’umanità ovvero il problema dello “spiaccicamento della sfera” che, espresso in modo più forbito, è il problema di come fare delle carte geografiche che si possano stendere su una tavola. L’amara verità è che nessuna triangolazione è mai esatta e quindi sfugge sempre qualcosa. Se si riescono a conservare le aree, non si riescono a conservare gli angoli tra le rette e viceversa. Se si tiene conto degli angoli allora le distanze scappano all’infinito oppure le linee rette diventano curve oppure non si conservano le direzioni.

Forse chi più di chiunque altro ha giustificato la necessità di conoscere le cifre di π, seppure indirettamente, è la poetessa polacca Maria Wisława Anna Szymborska (1923-2012), Premio Nobel per la letteratura 1996, che nella raccolta Numero enorme (Wielka Liczba) del 1976, scrisse la poesia Liczba Pi (Pi greco):

Podziwu godna liczba Pi
trzy koma jeden cztery jeden.
Wszystkie jej dalsze cyfry też są początkowe,
pięć dziewięć dwa ponieważ nigdy się nie kończy.
Nie pozwala się objąć sześć pięć trzy pięć spojrzeniem
osiem dziewięć obliczeniem
iedem dziewięć wyobraźnią,
a nawet trzy dwa trzy osiem żartem, czyli porównaniem
cztery sześć do czegokolwiek
dwa sześć cztery trzy na świecie.
Najdłuższy ziemski wąż po kilkunastu metrach się urywa.
Podobnie, choć trochę później, czynią węże bajeczne.
Korowód cyfr składających się na liczbę Pi
nie zatrzymuje się na brzegu kartki,
potrafi ciągnąć się po stole, przez powietrze,
przez mur, liść, gniazdo ptasie, chmury, prosto w niebo,
przez całą nieba wzdętość i bezdenność.
O, jak krótki, wprost mysi, jest warkocz komety!
Jak wątły promień gwiazdy, że zakrzywia się w lada przestrzeni!
A tu dwa trzy piętnaście trzysta dziewiętnaście
mój numer telefonu twój numer koszuli
rok tysiąc dziewięćset siedemdziesiąty trzeci szóste piętro
ilość mieszkańców sześćdziesiąt pięć groszy
obwód w biodrach dwa palce szarada i szyfr,
w którym słowiczku mój a leć, a piej
oraz uprasza się zachować spokój,
a także ziemia i niebo przeminą,
ale nie liczba Pi, co to to nie,
ona wciąż swoje niezłe jeszcze pięć,
nie byle jakie osiem,
nieostatnie siedem,
przynaglając, ach, przynaglając gnuśną wieczność
do trwania.

È degno di ammirazione il Pi greco
tre virgola uno quattro uno.
Anche tutte le sue cifre successive sono iniziali,
cinque nove due, poiché non finisce mai.
Non si lascia abbracciare sei cinque tre cinque dallo sguardo,
otto nove, dal calcolo,
sette nove dall’immaginazione,
e nemmeno tre due tre otto dallo scherzo, ossia dal paragone
quattro sei con qualsiasi cosa
due sei quattro tre al mondo.
Il serpente più lungo della terra dopo vari metri si interrompe.
Lo stesso, anche se un po’ dopo, fanno i serpenti delle fiabe.
Il corteo di cifre che compongono il Pi greco non si ferma sul bordo della pagina,
È capace di srotolarsi sul tavolo, nell’aria, attraverso il muro, la foglia, il nido, le nuvole,
diritto fino al cielo, per quanto è gonfio e senza fondo il cielo.
Quanto è corta la treccia della cometa, proprio un codino!
Com’è tenue il raggio della stella, che si curva a ogni spazio!
E invece qui due tre quindici trecentodiciannove
il mio numero di telefono il tuo numero di collo
l’anno millenovecentosettantatré sesto piano
il numero degli inquilini sessantacinque centesimi
la misura dei fianchi due dita sciarada e cifra
in cui vola e canta usignolo mio
oppure si prega di mantenere la calma,
e anche la terra e il cielo passeranno,
ma non il Pi greco,
oh no, niente da fare,
esso sta lì con il suo cinque ancora passabile,
un otto niente male,
un sette non ultimo,
incitando, ah, incitando
l’indolente eternità a durare.

(La traduzione è quella in Wisława Szymborska – Opere – Adelphi  2008)

In Cianfrusaglie del passato – La vita di Wisława Szymborska di Anna Bikont e Joanna Szczęsna (Adelphi – 2015) è riportato: “Qualche giorno dopo, all’incontro di Udine, il sindaco ed ex rettore della locale università, il matematico Furio Honsell, volle leggere pubblicamente la poesia, Pi Greco.” Si tratta della Festa del π del 2015 a Udine. Per illustrare la poetica di Szymborska, che ritorva l’universo nelle cifre di π leggendole come una sciarada, mi limito a tradurre due frasi.

La prima è tratta dalla motivazione del Nobel. “..for poetry that with ironic precision allows the historical and biological context to come to light in fragments of human reality.” (…per una poesia che con precisione ironica permette al contest storico e biologico di venire alla luce sotto forma di frammenti di una realtà umana.)

La seconda è tratta dal suo discorso di accettazione al Nobel. “But ‘astonishing’ is an epithet concealing a logical trap. We’re astonished, after all, by things that deviate from some well-known and universally acknowledged norm, from an obviousness we’ve grown accustomed to. Now the point is, there is no such obvious world. Our astonishment exists per se and isn’t based on comparison with something else. Granted, in daily speech, where we don’t stop to consider every word, we all use phrases like “the ordinary world,” “ordinary life,” “the ordinary course of events” … But in the language of poetry, where every word is weighed, nothing is usual or normal. Not a single stone and not a single cloud above it. Not a single day and not a single night after it. And above all, not a single existence, not anyone’s existence in this world.” (Ma ‘meraviglioso’ è un epiteto che nasconde un tranello logico. Siamo meravigliati, dopo tutto, da cose che deviano da una norma ben nota o universalmente riconosciuta, da un’ovvietà a cui ci siamo abituati. Ora il punto è questo, non esiste un tale mondo ovvio. La nostra meraviglia esiste per se e non si basa su confronto con qualcosa d’altro. È vero, nel parlare quotidiano, dove non ci fermiamo a considerare ogni parola, usiamo frasi come ‘nella realtà ordinaria’, ‘vita quotidiana’, ‘il naturale corso degli eventi’… Ma nel linguaggio poetico, nel quale ogni parola è soppesata, nulla è consueto o normale. Non una singola pietra o una nube in alto sopra ad essa. Non una singola giornata non una singola notte successiva. E soprattutto non una singola esistenza, non l’esistenza di chiunque a questo mondo). Penso che queste parole abbiano la forza di dare dignità anche ad ogni singola cifra di π, anche se dopotutto, come disse Goethe: l poeta sa che cosa voleva scrivere, ma non sa che cosa ha scritto.

Concludo con un problemino, per farvi asciugare le lacrime di commozione di fronte alla poesia. Se è impossibile quadrare il cerchio, non tutte le aree con bordi curvi hanno però superfici che non si possano esprimere in modo razionale.  Sapendo che il diametro dei cerchi è 1 quanto misura la superficie dell’area rossa?

Infine, spero di avervi convinto che conoscere le cifre di π è importante, perché come disse la poetessa: le cifre di π si susseguano incitando, oh sì, incitando la pigra eternità a durare.